PHYSICS ENVY AMONG BIOLOGISTS: FACT OR FICTION?
Physicists often state their belief that all biologists would rather be physicists, but became biologists only because they were not very good at math. As evidence for this, they point to such findings as the fact that the vast majority of published studies in virology, cell biology, endocrinology, and even microbiology, use few if any partial differential equations or elements of number theory, and only one paper written by a biologist in the past 25 years (in the field of neurophysiology) has ever used tensor calculus.
On the surface, this would seem to be a damning indictment of biology. Why, physicists ask, do biologists seem unable to utilize such simple concepts as the Riemannian-Christoffel curvature tensor or Galois fields in their work?
I discussed this issue of alleged innumeracy among biologists with a physicist friend of mine a few weeks ago while he was driving me to the airport in his cab. Inevitably, however, the discussion turned to possible collaborative experiments which would combine physics and biology.
In one such experiment, we considered the possibility of accelerating two rats to relativistic velocity, and smashing them together and counting the rat particles that would be emitted. For a time, there appeared to be the exciting possibility of discovering a new elementary particle, which would be found only in living matter, and which could tie the field of quantum mechanics with the emerging biological science of consciousness. However, with the help of the formidable mathematical skills of another physicist friend, we were able to estimate that the number of rat particles emitted would probably be too large to count [1], even if we put all our NIH postdocs on the problem. In fact, it would be too many even if our Howard Hughes fellows and all of our Summer Students pitched in and contributed their formidable math skills as well to the project. Thus, the elusive consciousness particle would have been impossible to detect.
The great enthusiasm expressed for this experiment by my physicist friend, however, revealed an important and surprising fact. When pressed, many physicists will reveal in confidence that they would actually rather have been biologists, but for the unfortunate fact that they were unable to keep anything alive long enough to study it. This is particularly true of subatomic physicists. Many researchers in the physical sciences in particular seem to be genuinely distressed about this, and in some cases their work reveals subtle psychological doubts, conflicts, and uncertainties about their inability to keep things alive. The well-known case of Schrodinger and his cat provides a perfect example.
But is there any real scientific truth to the assertion that physicists have trouble keeping things alive? In a famous study [2], the ability of prominent physicists from various subdisciplines to maintain a culture of bacteria was studied. The physicists were instructed to streak an agar plate with E. coli bacteria. The cells were then analyzed at different times and the percentage of bacteria still alive were counted using a computer program. The parts of the program that had math that was too hard were written with the aid of an ex-physicist. Although bacteria are hardy creatures, and tend to grow in great abundance without assistance, the longest survival time of any bacterium in the hands of a nuclear physicist was only 17 minutes and 18 seconds. Solid state physicists performed better, at 21 min 45 sec, while bacteria in the hands of astrophysicists survived a mere 12 minutes and 58 seconds. These are dismal numbers indeed, and point to a widespread incellularosity among all branches of physics.
It has been proposed that the roots of this phenomenon of incellularosity may be found in the early education of physicists. Indeed, in a follow-up study [3], a detailed analysis of the ill-fated Petri plates showed that, in many cases, the tragic deaths of all those millions of E. coli could be attributed to what, to biologists, may seem like relatively simple errors. For example, in one case, the plate was incubated at 1,700,000 degrees, a temperature far in excess of the optimal growing temperature for bacteria of 37 degrees Centigrade. In another case, it was found that the plate had not been streaked at all. The bacteria from this plate have never been recovered, and it is still not known precisely where the physicist streaked his bacteria. Unfortunately, the physicist in question could not be queried on this point, as he has sadly passed away after a sudden and unexpected illness.
A significant statistical problem encountered during this study, however, was that several of the physicists, rather than remaining to complete the test, made what the authors termed “disparaging remarks” about the authors’ experimental design, and returned to their laboratories, where they wrote detailed papers describing the mathematical underpinnings of bacterial cell division. Even worse, two of the physicists subsequently went on trips to Oslo, Norway as a result of this, and the remainder refused to return phone calls from the authors. Thus, the results were skewed in favor of slightly “less-obnoxious” physicists.
Another statistical problem that was noticed was that no theoretical physicists had been included in the experiment. In fact, the authors, after desperate attempts to locate some theoretical physicists, ultimately concluded that such physicists did not, in fact, exist. The existence of such scientists had been postulated years earlier by Ashimoto et al.[4], but as of this writing, none has ever been observed. Thus, this branch of physics remains largely theoretical. As a famous biologist once remarked, “this is just as well, as theoretical physics is mostly just a bunch of complicated math stuff anyway.”
Yet as revealing and touching as these anecdotal stories may be, the grim spectre of incellularosity needs to be taken seriously. Therefore, we will leave this topic for someone else and switch back to our original topic, that of the mathematical abilities (or absence thereof) in biologists.
Many anthroponumerical studies have focused on biologists, particularly in relation to their difficulties with left-brain skills such as mathematical reasoning and 3D spatial ability. Zubiaga et al. [5] reported that biologists, accustomed to rounded, natural shapes, had great difficulty in tasks requiring strong 3D visualization of flat, rectilinear-shaped objects, such as assembling cardboard broken glass disposal boxes. Their photos of tragically misshapen biohazard boxes assembled by frustrated and exhausted biologists, and broken-glass boxes assembled upside-down and held together with autoclave tape, are quite revealing. Zubiaga, a renowned particle physicist himself, speculated that other similar complex three-dimensional objects, such as lawn chairs, could well suffer a similar fate.
In actuality, the unfortunate fact that cell division and multiplication are synonymous has long been a cause of great mathematical angst among biologists, who after a long day watching cells increasing in number after dividing, often find themselves getting the x and / keys on their calculators confused.
Russell[6] documented the now well-accepted finding that biologists rarely use integers per se, particularly when making chemical solutions. When they believe themselves to be unobserved, biologists prefer to use their own unique counting system consisting of the following quantities:
1. Some.
2. A bunch.
3. A whole bunch.
4. All of it.
5. See if somebody else has any.
6. We’ll have to buy some more.
7. Let’s write a new grant.
These quantification terms are roughly delineated by increasing powers of 10. The biologists’ counting system was compared to the primitive counting system used until quite recently in Samoa. However, Rascher[7] has claimed that subsequent interviews with the native subjects who had provided cultural information in the initial Samoan study, revealed that the Samoans actually thought the original anthropologist was just ‘kidding around’, and were merely cracking jokes about their counting system. According to Rascher, Samoan society did not use a primitive counting system after all but were in fact mathematically highly advanced, having actually developed differential calculus over 500 years before Newton.
The biologists’ counting system has been defended by Baber, who noted that the system used by biologists is significantly more accurate than calculations performed on advanced state-of-the-art software such as Microsoft (TM) Excel [8]. Baber also claimed that, like the ancient Mayans, biologists appeared to have developed their own calendar, which was more accurate than the calendar on some modern-day computers (e.g., the AT&T 6300). However, no additional details of this potentially important finding were provided in Baber’s book[8], and other researchers have recently disputed this claim.
Footnotes:
[1] Using the biologists’ numbering system, he estimated that the total number of particles would be
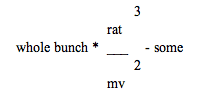
This is obviously higher that we, as mere biologists, could possibly count, and the sight of the exponent in this very complicated-looking equation served to dissuade us of the entire concept.
[2] Rosenberg, J. et al., Soc. Psych. Biol. Phys. 1, 14 (1996).
[3] Rosenberg, J. et al., J. Unpublished Results 33, 14705 (1998).
[4] Ashimoto, Watashino, personal communication.
[5] Zubiaga, T., Lebovic, V., and Vlasek, P., Czech. J. Unpub. Results 22, 143 (1988).
[6] Russell, R., personal communication.
[7] Rascher, R. and Nolan-Rascher, B., personal communication.
[8] Baber, B., in Excel for Blithering Morons, Wipburn Press, p. 1479 (1999).